I love back of envelope calculations and I love Rachel Maddow, she is so bright and usually does her homework. Yesterday, not so much. In this segment:
she completely screws up a back of envelope calculation on how many deaths might happen before we get to herd immunity. She starts out correctly: if you use the standard “threshold theorem” 1 , you conclude that roughly 65% of the people (roughly 215,000,000) need to be infected and become immune before you get to herd immunity.
And then she goes completely off the rails. She says there are about 6.6 million confirmed cases of Covid-19 with about 200,000 deaths, so there is a case fatality rate of about 2.97% based on the total number of cases (roughly 200,000/6,600,00). That’s correct. And then this graphic shows up:
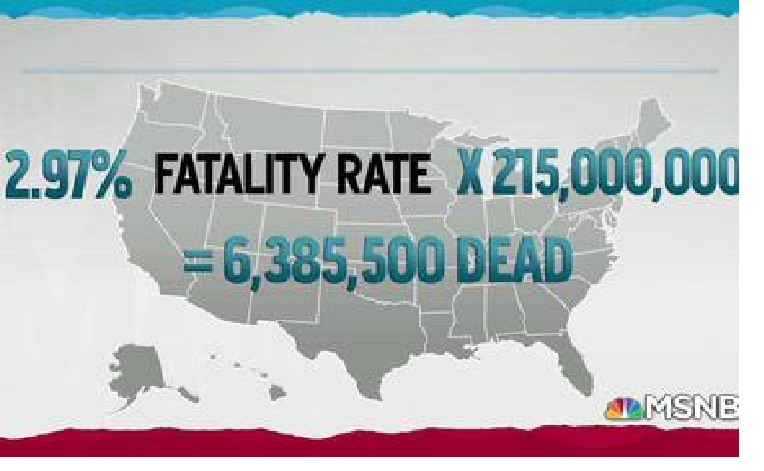
What she is doing here is taking the case fatality rate and multiplying it by the number of cases you would (roughly) need to have herd immunity. The problem is that you need to use the infection fatality rate not the case fatality rate in any calculation like this. And, because there are many many cases of Covid 19 that we don’t know about than those we have found through testing, these two numbers are very different. The infection fatality rate is much much lower. Why didn’t she check with Ashish Jha or Michael Osterholm who would have caught this horrible mistake? The good guys aren’t supposed to go so badly off the rails.
Look anyway you cut it, as I will shortly show you, the number of deaths is beyond horrible. But using the case fatality rate rather than the infection fatality rate means the number of deaths is too high by at least a factor of 3 – and that is absent any therapeutic changes which she correctly points out later would lower this number.
So what was her mistake? Well, the 6.6 million confirmed cases are just the tip of the iceberg. Based on antibody testings (and of course the test positivity ratios we have seen) the best estimates of the number of infections in the United States I have seen say there are between three and twelve times the number of infected people as there are confirmed cases i.e. roughly between 20 and 80 million people have actually been infected by Covid 19. Using these numbers you get an infection fatality rate of between .25% (200,000/80,000,000) and 1% (200,000/20,000,000). Anthony Fauci thinks that the infection fatality rate is actually the higher number i.e. about 1%, so I will use this number. This rate gives us (absent any therapeutic changes that greatly lower the death rate) 2.15 million deaths (1%*215,000,000) before herd immunity occurs at the high end with Fauci’s estimate and about 550,000 at the low end if the infection is far more widespread than testing would indicate.
So, the situation is beyond horrible in both cases – if we take the herd immunity route, but let’s not do the math wrong – it gives ammunition to the bad guys.
Regarding the following: “She says there are about 6.6 million confirmed cases of Covid-19 with about 200,000 deaths, so there is a case fatality rate of about 2.97%. That’s correct.”
That’s not correct. According to the Worldometer website, there are 6.6 million total cases but only 4.3 million closed cases (those with an outcome). So there are about 2 million cases ‘in progress’ where the fatalities are yet to be determined. Closed cases is the accurate data, and the closed case fatality rate is 5%.
However, as noted, the actual total cases are estimated at 6 to 24 times the known cases. Using 15 times the 4.3 million known closed cases to estimate actual closed cases, the fatality rate is 200,000/(15×4.3 million) = 0.31%. If herd immunity is achieved at 65% of the US population, the total fatalities would be 0.0031×0.65x330mil = 665,000.
I did not read the paper about a lower percentage for herd immunity, but I would expect masks and minimizing contact with others allows the virus to die out at less than 65% as these mitigations, in essence, increase the immune population.
The unknown cases is the wild card in predicting total fatalities. With only 200,000 fatalities to date, the US appears to have a long way to go without a vaccine.
Good points all!
While I find your use of “good guys” and “bad guys” somewhat jarring, as a fellow mathematician I felt compelled to comment, because while your approximation fixes the stupid mistake from TV, it is still wrong.
a) There is no single IFR. The IFR is a function of (amongst other things) how good your treatment is, how strong your immune system is (which may depend on the time of year), which strain of the virus you get, and much more. You write “absent any therapeutic changes that greatly lower the death rate”, but isn’t it widely accepted that we are seeing lower deaths, at least amongst the hospitalized? I’ve seen several articles like https://www.bbc.com/news/health-53192532 . Given that survival rates in hospitals are improving (according to some studies, by a factor of over 2 times (!)) this is significant.
b) There is no single “herd immunity threshold”, as (as you surely know) the SIR model is overly simplistic. The comment by Russ above addresses this.
c) There is also the fact that many people may have some immunity even without being infected – see e.g. the work of Friston on “immunological dark matter”.
I’d love to believe the more sophisticated Rt based/super spreader models for Covid 19 transmission are correct (see for example: https://www.medrxiv.org/content/10.1101/2020.05.19.20104596v1.full.pdf)
The math sure is pretty and obviously much more interesting than the high school math needed to prove the “Threshold Theorem”. But it seems Manaus in Brazil is a counterexample to them. Ironically. it seems that the naive threshold theorem (1-1/R0) may work better